HOLISMOKES. VII. Time-delay measurement of strongly lensed SNe Ia using machine learning

We present two machine learning approaches to measure time delays in LSNe Ia, namely, a fully connected neural network (FCNN) with two hidden layers and a Random Forest (RF; Breiman 2001). For the training of the FCNN and the RF, we simulate mock LSNe Ia from theoretical SN Ia models (Nomoto et al. 1984; Sim et al. 2010; Pakmor et al. 2012; Seitenzahl et al. 2013), where synthetic observables have been calculated using ARTIS (Kromer & Sim 2009). Further, we include observational noise (LSST Science Collaboration 2009) and microlensing (Yahalomi et al. 2017; Goldstein et al. 2018; Foxley-Marrable et al. 2018; Huber et al. 2019; Pierel & Rodney 2019; Huber et al. 2020) using GERLUMPH (Vernardos et al. 2015) in our SN Ia light curves.

We test the generalizability of the machine learning models, by using a final test set based on empirical LSN Ia light curves from the SNEMO15 model (Saunders et al. 2018) not used in the training process, and we find that only the RF provides low enough bias to achieve precision cosmology, which is therefore preferred to our FCNN approach for applications to real systems.

For the RF with single-band photometry in the i-band, we obtain an accuracy better than 1% in all investigated cases for time delays longer than 15 days, assuming follow-up observations with a 5σ point-source depth of 24.7, a two day cadence with a few random gaps and a detection of the LSNe Ia 8 to 10 days before peak in the observer frame. In terms of precision, we can achieve under the same assumptions on the i band ~1.5 days uncertainty for a typical source redshift of ~0.8.

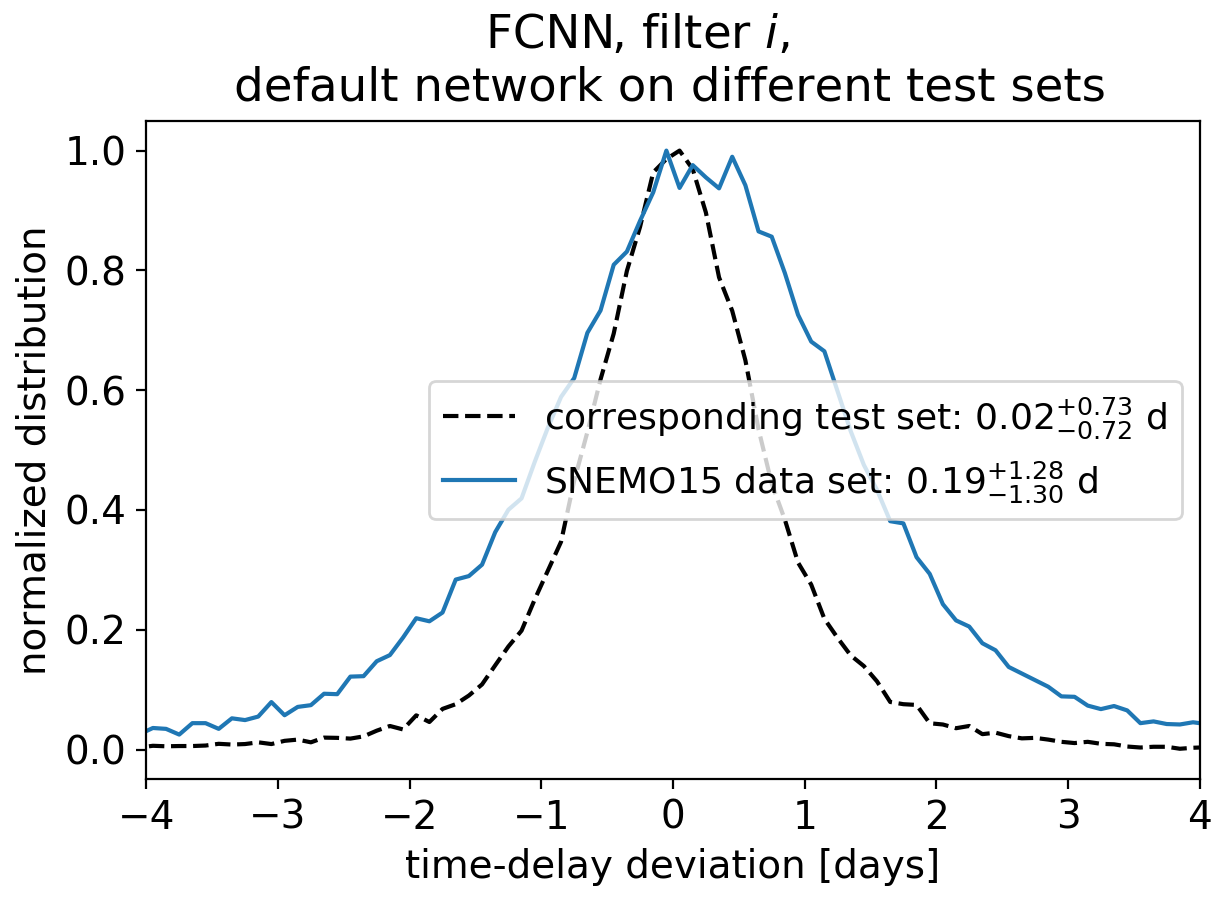
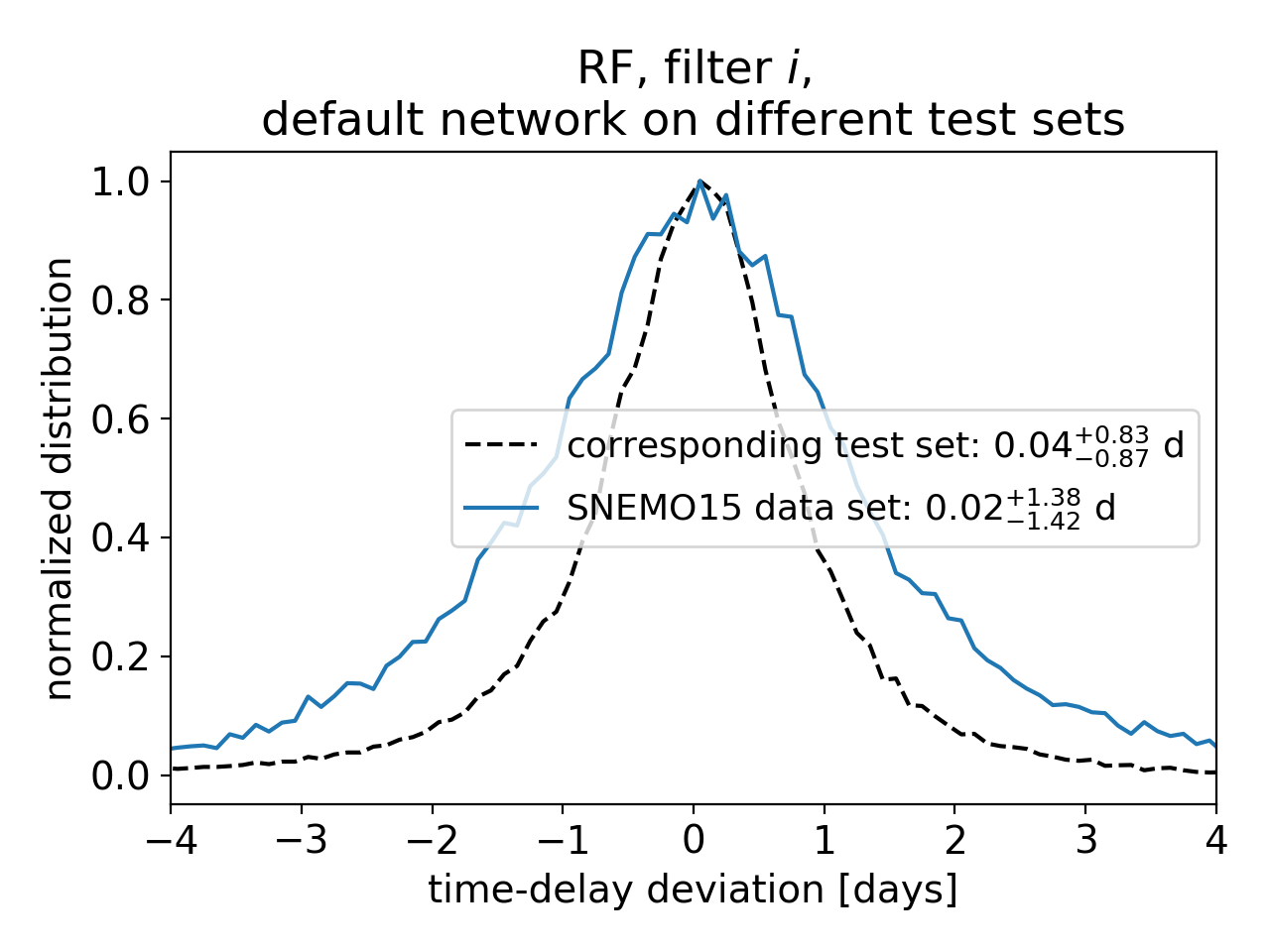
To improve the measurement we find that three bands, where we train a RF for each band separately and combine them afterwards, help to reduce the uncertainty to ~1.0 day. The three most promising filters to target are g,r, and i for z_s ≤ 0.6 and r,i, and z for z_s ≥ 0.6, where we aim for a single-epoch 5σ depth of at least 25.7, 25.3, 24.7, 23.8 for g,r,i, and z. The dominant source of uncertainty is the observational noise and therefore the depth is an especially important factor when follow-up observations are triggered.

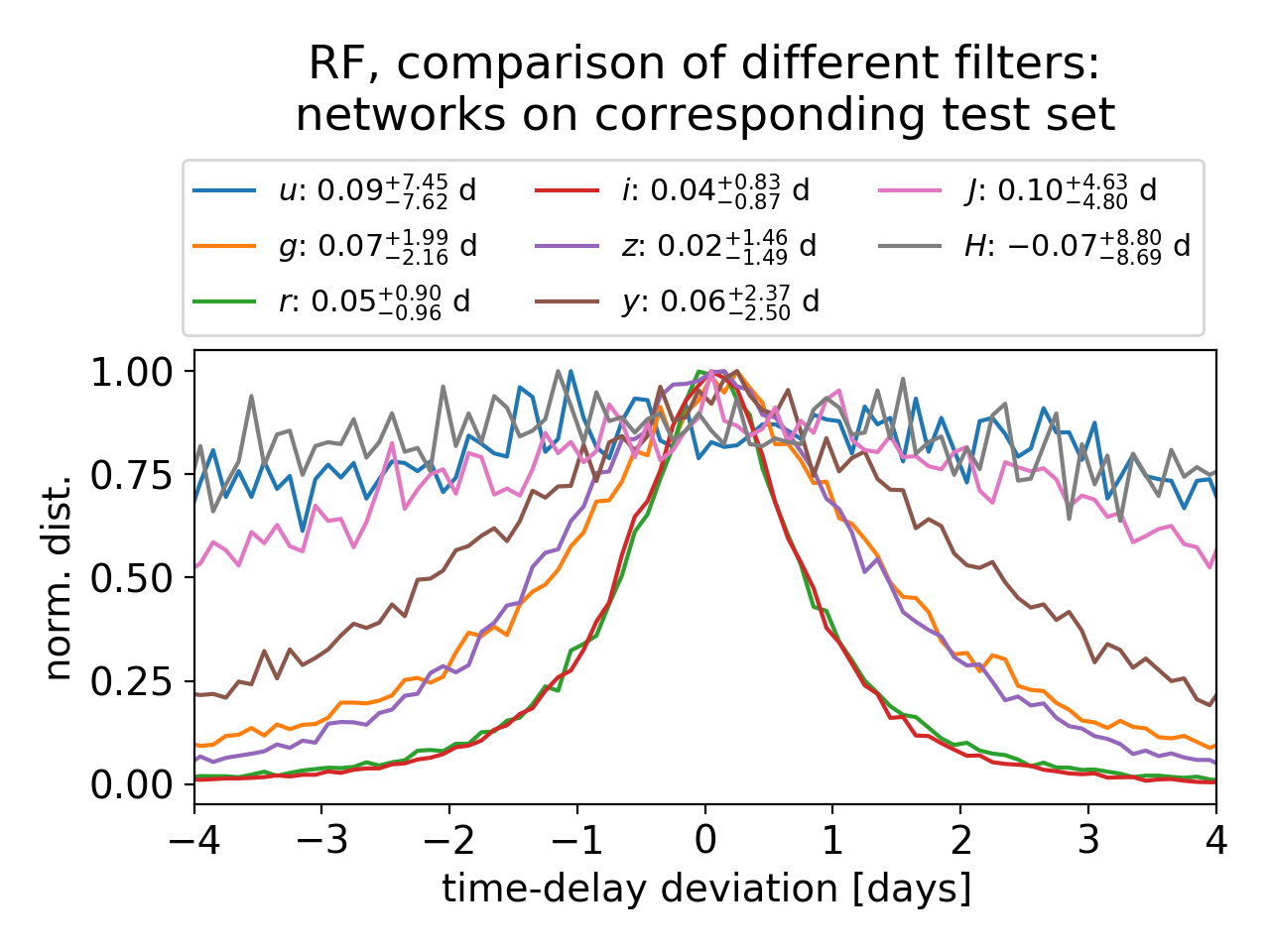
The weakness of this approach is that we need to train a ML model for each observed LSNe Ia individually, but the advantage is that we can train our model very specifically for the observation pattern, noise and microlensing uncertainties.