H0LiCOW V. New COSMOGRAIL time delays of HE0435−1223: H₀ to 3.8% precision from strong lensing in a flat ΛCDM model.

We present a new measurement of the Hubble Constant H₀ and other cosmological parameters based on the joint analysis of three multiply-imaged quasar systems with measured gravitational time delays. The “time-delay distances” in gravitationally lensed quasar systems offer an opportunity to measure H₀ independently of any other cosmological probe. First suggested by Refsdal (1964), this approach involves measuring the time delays between multiple images of a distant source produced by a foreground lensing object.

The COSMOGRAIL collaboration (COSmological MOnitoring of GRAvItational Lenses) has been monitoring about 20 lensed quasars with 1m-class and 2m-class telescopes since 2004 (see e.g. Courbin et al. 2005; Eigenbrod et al. 2006a; Bonvin et al. 2016). In this work, we use COSMOGRAIL data in collaboration with the Kochanek et al. (2006) team. The data acquired from autumn 2003 to spring 2010 were presented in Courbin et al. (2011). Here, we double the monitoring period, adding observations taken between autumn 2010 and spring 2016. Our monitoring sites include two Northern telescopes: the 1.2m Belgian Mercator telescope located at the Roque de Los Muchachos Observatory, La Palma, Canary Islands (Spain) and the 1.5m telescope located at the Maidanak Observatory (Uzbekistan). In the Southern hemisphere, the Swiss 1.2m Euler telescope located at the ESO La Silla observatory (Chile) has monitored HE0435−1223 since 2004. We also make use of the data obtained at the 1.3m SMARTS ANDICAM camera at Cerro Tololo Inter-American Observatory.

Given the limited photometric precision of the COSMOGRAIL images, long-term monitoring with good enough temporal sampling is crucial to the time delay measurement, for two main reasons. First, one needs to catch enough intrinsic photometric variations in the quasar light curves in order to identify common structures. Second, the extrinsic variability related to microlensing must be taken into account (e.g. by modeling and removing it) to avoid time-delay measurement biases. The availability of decade long light curves allows us to check for potentially significant biases by analysing subsets of the full data, and certainly to reduce residual ones.

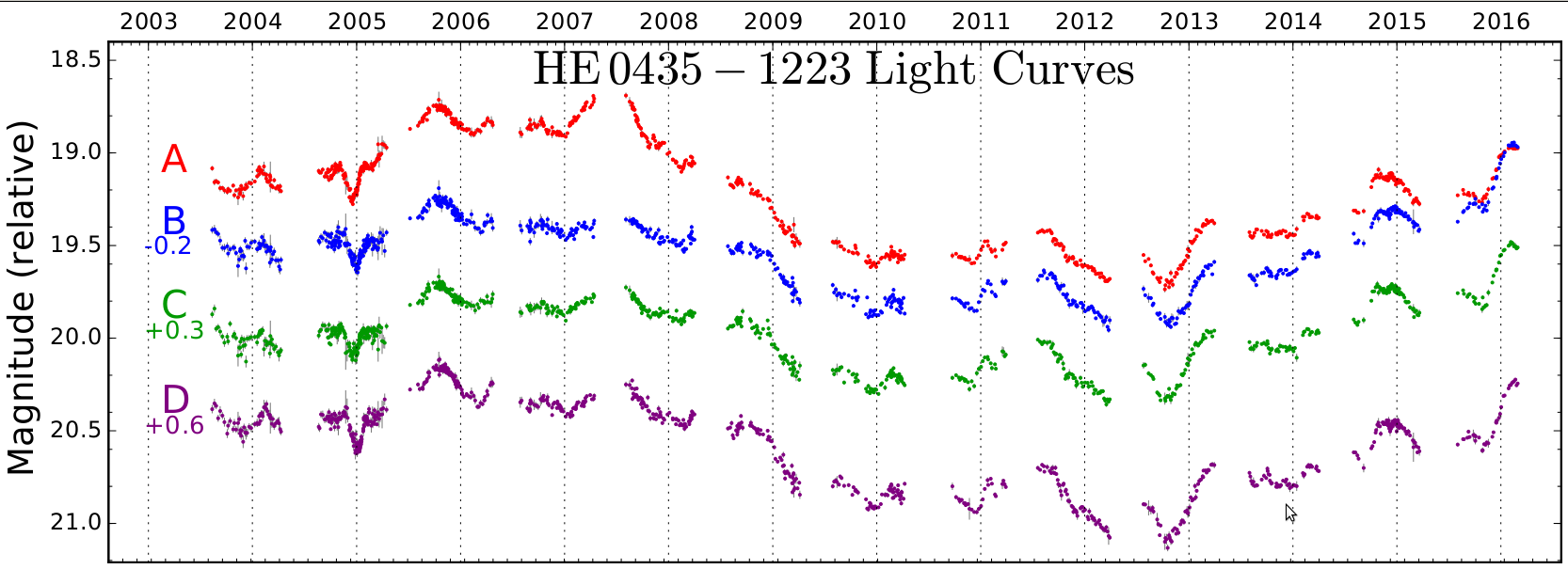
With the 13-year light curves in hand, the time delays can be measured using numerical techniques accounting for noisy photometry, irregular temporal sampling and seasonal monitoring gaps. Different techniques have been devised in the literature to carry out this task, and the COSMOGRAIL collaboration has implemented its own approach and several algorithms (Tewes et al. 2013a). These techniques are publicly available as a python package named PyCS. They have been tested using realistic numerical simulations, and have been confronted with the data provided to the lensing community by the first Time-Delay Challenge (TDC1; see Dobler et al. 2015; Liao et al. 2015). An in-depth analysis of their performance proved them to be both precise and accurate (Bonvin et al. 2016) under various observational conditions, and in particular for light curves mimicking the COSMOGRAIL data.

In this work, we consider two algorithms:

• The free-knot spline technique, that models the light curves through a simultaneous fit of the intrinsic variations of the quasar, common to the four light curves, summed with some extrinsic variability different in each of the four light curves. All curves are represented as free-knot splines (see e.g. Molinari et al. 2004), for which the knot locations are optimised at the same time as the spline coefficients and the time shifts.
• The regression difference technique, that minimises the variability of the difference between Gaussian-process regressions performed on each light curve. This method has no explicitly parametrised model for extrinsic variability. Instead, it yields time-delay estimates which minimize apparent extrinsic variability on time scales comparable to that of the intrinsic variability features.

A key ingredient of the time-delay measurement is the careful generation of mock light curves which are used to fine-tune and assess the precision and bias of the point estimators. These simulations are fully synthetic, in the sense that they are drawn from models with known time delays and yet they closely mimic the quasar variability signal and the extrinsic variability from the observed data. We made them publicly available, as well as the observed light curves at the bottom of this page.

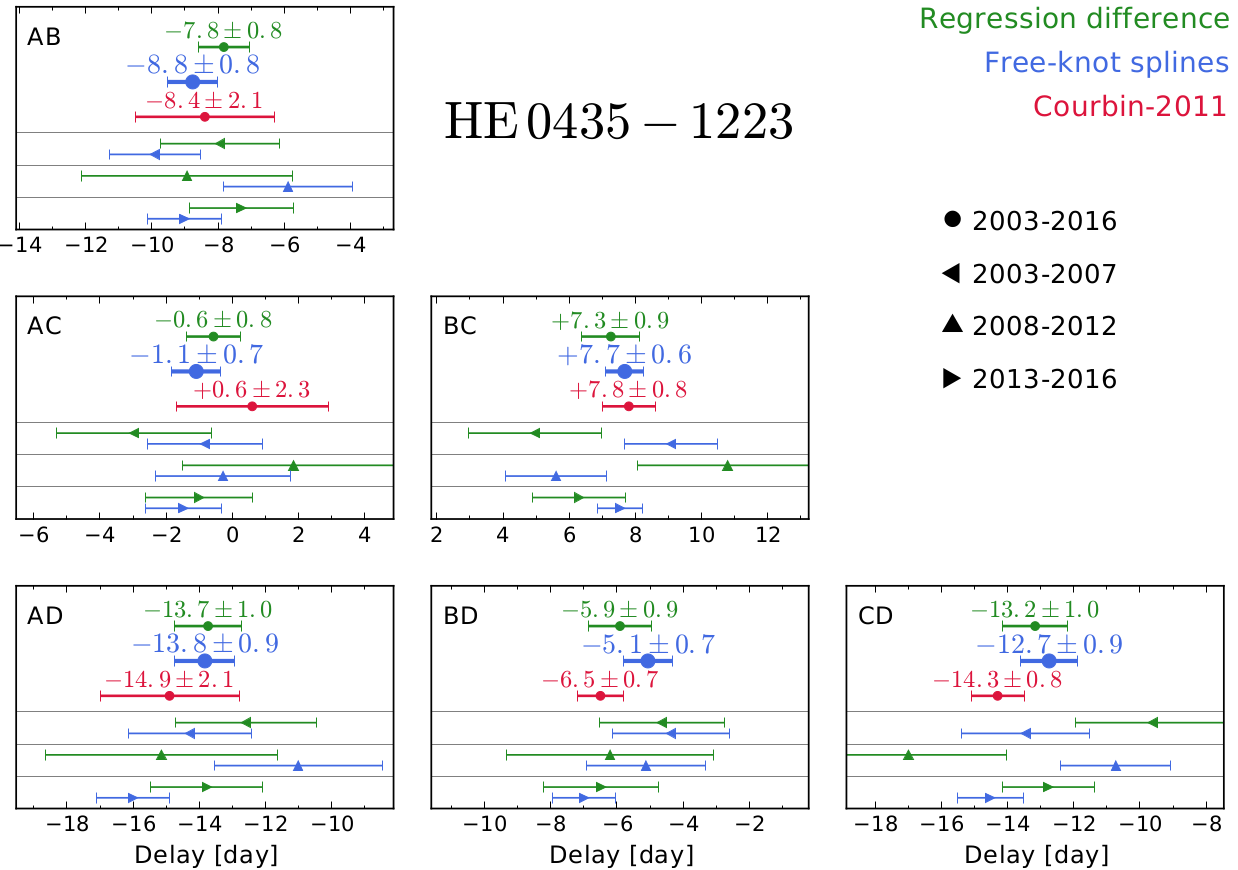
These time delays, combined with a careful modeling of the lens galaxy mass distribution, can be used to infer the time-delay distance in the HE0435−1223 system. The lens modeling and time-delay distance determination are addressed in detail in H0LiCOW Paper IV. In this work, we present our inference of the cosmological parameters obtained using the time-delay distance of HE0435−1223, combined with our previous works on the systems B1608+656 (Suyu et al. 2010) and WFI2033−4723 (Suyu et al. 2013, 2014). We combine these three lenses in a so-called Time-Delay-Strong-Lensing probe (TDSL).

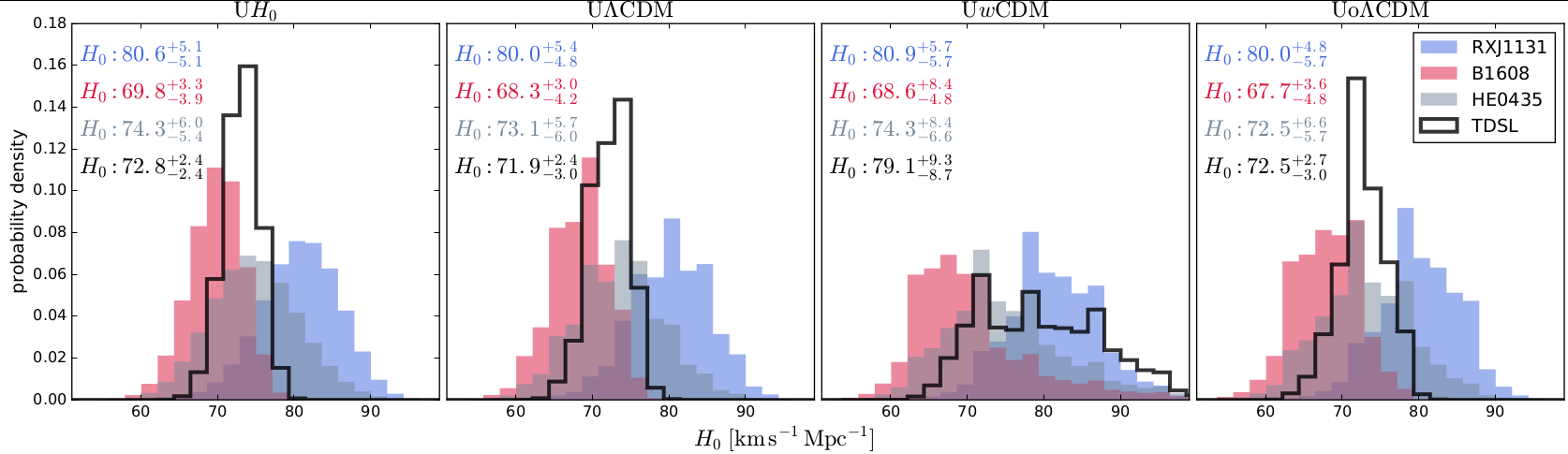
We first present our values for the cosmological parameters that can be inferred from TDSL alone. Our baseine model, UH₀, has a uniform prior on H₀ in the range [0, 150] km/s/Mpc, a matter density fixed at Ωm = 0.32 from the most recent Planck results (Planck Collaboration et al. 2015a), zero curvature Ωk = 0 and consequently a fixed cosmological constant. This model has only one free parameter. From left to right in the figure below, we present this UH₀ cosmology, and then three models that have two or three free parameters (H₀ plus one or two others): the UΛCDM cosmology where we allow Ωm to vary with uniform prior; the UwCDM cosmology with a free Ωde and a free time-independent dark energy equation of state w, both with uniform priors; and finally the UoΛCDM cosmology, that relaxes the constraint on the curvature Ωk and allows both this and ΩΛ to vary with uniform priors. We quote in each panel the corresponding median and 1σ uncertainties of H₀.

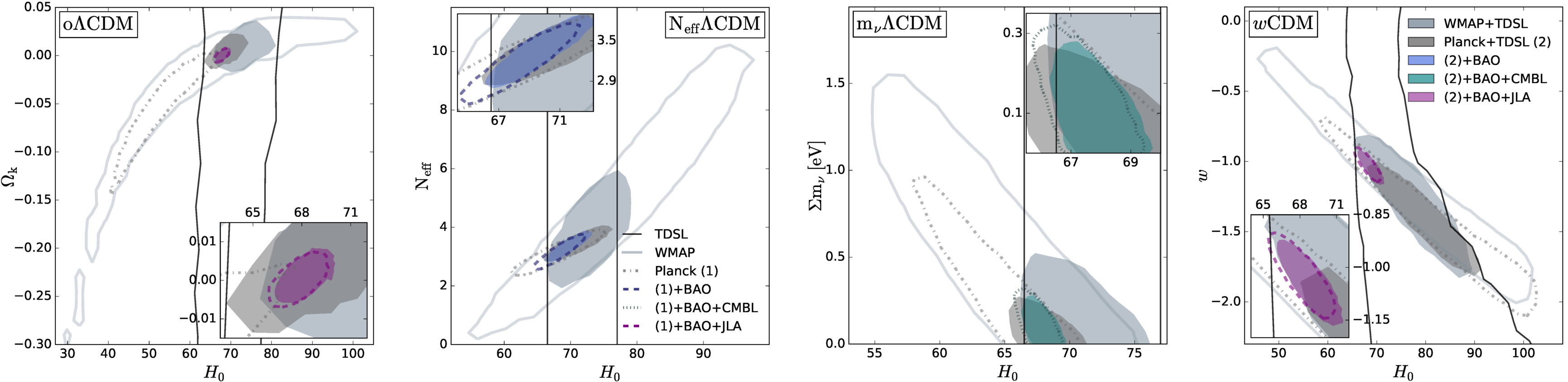
We explore more general cosmological models combining TDSL with other probes, illustrating its power to break degeneracies inherent to other methods. We present in the Figure below the 95% credible regions in the two-dimensional marginalized parameter space for a selection of cosmological models for which the impact of TDSL is the most meaningful. In the oΛCDM model, we consider a non-flat Universe with variabl Ωk. In the wCDM model we consider a time-invariant dark energy equation of state w. In the NeffΛCDM model, we consider a variable effective number of relativistic neutrino species Neff with a fixed total mass of neutrinos Σmν = 0.06 eV. Finally, in the mνΛCDM model we consider a variable Σmν with a fixed Neff = 3.046. The TDSL and Planck joint constraints are H₀ = 69.2 +1.4 -2.2 km/s/Mpc, ΩΛ = 0.70 +0.01 -0.01 and Ωk = 0.003 +0.004 -0.006 in oΛCDM and H₀ = 79.0 +4.4 -4.2 km/s/Mpc, Ωde = 0.77 +0.02 -0.03 and w = -1.38 +0.14 -0.16 in flat wCDM. Combined with Planck and Baryon Acoustic Oscillation data, when relaxing the constraints on the numbers of relativistic species we find Neff = 3.34 +0.21 -0.21 and when relaxing the total mass of neutrinos we find 0.182 eV.

The combined strengths of our H0LiCOW lens modeling and COSMOGRAIL monitoring indicate that quasar time-delay cosmography is now a mature field, producing precise and accurate inferences of cosmological parameters, that are independent of any other cosmological probe. Our future plans are to enlarge the sample of H0LiCOW lenses. In particular, two more objects with excellent time-delay measurements as well as high-resolution imaging and spectroscopic data remain to be analysed. When completed, H0LiCOW is expected to provide a measurement of H₀ to better than 3.5% in most cosmological models.

In addition, we also continuously improve our treatment of each of the key steps of the time-delay distance technique:

• Improve the lens modeling accuracy. As the number of systems being analysed grows, random uncertainties in the cosmological parameters will fall, and residual systematic uncertainties related to degeneracies inherent to gravitational lensing will need to be investigated in more detail.
• Improve the absolute mass calibration. Spatially resolved 2D kinematics of the lens galaxies, to be obtained either with JWST and with integral field spectrographs mounted on large ground-based telescopes with adaptive optics, should further improve both the precision for each system and our ability to test for residual systematics, including those arising from the mass sheet and source position transformations.
• Increasing the monitoring efficiency, by catching extremely small (mmag) and fast (days) variations in the quasar light curves. Such data can be obtained with daily observations with 2-m class telescopes in good seeing conditions, a project implemented in the context of the COSMOGRAIL program (e.g. Courbin et al. 2017)